| descartes-src (ソースパッケージ descartes-src-0.26.0.tar.gz) | 2012-09-09 20:57 |
| descartes-win (Windows用バイナリパッケージ descartes-win-0.26.0.zip) | 2012-09-09 20:52 |
| 会話キャラクター: ツンデレ アプリケーション (会話キャラ:ツンデレ v1.0 for Windows) | 2010-04-29 13:41 |
| 会話キャラクター: 2人の女の子 ダブルキャラクター (会話キャラクター 2人の女の子 ダブルキャラクター 1.0 for Windows) | 2011-10-02 22:23 |
| 会話キャラクター: Eliza風英語版 (会話キャラ:Eliza風英語版 v1.0 for Windows) | 2010-05-11 01:06 |
| 会話キャラクター: 猫耳メイド アプリケーション (会話キャラ:猫耳メイド v1.0 for Windows) | 2010-04-27 21:15 |
| 会話キャラクター: イライザ風日本語版 (会話キャラ:イライザ風日本語版 v1.0 for Windows) | 2010-04-30 21:53 |
| 経済指標表示プログラム for Windows (経済指標表示プログラム V1.0) | 2011-08-18 22:04 |
| ニュースヘッドライン表示プログラム (ニュースヘッドライン表示プログラム V1.0 for Windows) | 2011-08-16 12:31 |
| デカルト言語 example (デカルト言語の例題 example-0.7.0.zip) | 2009-03-01 19:47 |
| 電力状況表示プログラム for Windows (2011年夏版 全国電力供給状況表示プログラム V1.0) | 2011-08-15 13:25 |
ランチェスター理論は、イギリスのフレデリック・ウィリアム・ランチェスター(Frederick William Lanchester, 1868-1946)によって唱えられた戦闘の数理モデルです。
(余談ですがランチェスターの生まれた1868年は、日本では王政復古の大号令が出て、鳥羽伏見の戦いがあり、戊辰戦争が始まり、江戸城開城があり、明治維新が成立した戦乱と激動の年です。)
ランチェスターは、第一次大戦の戦闘の研究からランチェスターの法則を発見しました。
この法則では2つの異なる戦闘部隊の戦力の戦いにおける兵力数の変化を説明します。
なお、ランチェスターの法則には第1法則と第2法則があります。とくに第1法則は「一騎討ちの法則」、第2法則は、「戦力2乗則」とも呼ばれ有名です。
現在では、ランチェスター理論は経営学にもさまざまに解釈されて応用されています。
ランチェスターの第1法則は、一騎討ちの法則とも呼ばれるもので、敵味方が一対一で戦う場合に起こる状況について説明する法則です。
古代の戦いのように刀剣で戦う場合で、相手を探して戦いを挑み、剣をカンカンと何度も打ち合わせて交えながら押し引きして戦闘を行うシーンを想像してください。
たとえ隣で戦っている敵がいるとしても、今一瞬でも目の前の敵から注意をそらせば自分が斬られます。また激しく斬激を繰り返しながら動きまわる敵味方には、他の人間が割り込むのも大変だったのではないでしょうか。
このような状況では一騎討ちの戦闘が主体となって発生するでしょう。
つまり、このような一騎討ちでは、どうしても大軍のほうが戦力が余ってしまい、戦いに参加しきれない遊兵が発生してしまうことでしょう。
ランチェスターの第1法則は、このような一騎討ちの戦闘をモデル化します。
ランチェスターの第2法則は、「戦力2乗則」とも呼ばれるもので、敵と味方が銃や大砲などを使い、集団対集団で戦う場合に起こる状況について説明する法則です。
銃や大砲などを使うと、1人が一度に複数の敵を攻撃することができるようになります。 近代から現代に至る戦いでは、このような兵器を使い広域での戦いが主流となりました。このような集団戦では、大軍は敵より数が多くても余ることなく少ない敵に集中的に損害を与えることができるようになります。
ランチェスター理論が画期的に優れた理論だったのは、いずれか一方が戦闘不能になるまで戦闘を続ければ、残りの兵力がどうなるかを明確に示したことです。
ランチェスターの第1法則では、戦闘の結果は双方の戦力を引き算することで残存戦力を予測することが出来るモデルとなります。
例えば、X軍の10人とY軍の8人で戦うとします。 この結果は、一人ずつの一騎討ちなので、10 - 8 = 2ということで、多勢の兵が2人残るということです。
式で表すと以下のようになります。
(x0 - x) = (y0 - y) x0: X軍の初期戦力 x : X軍の残存戦力 y0: Y軍の初期戦力 y : Y軍の残存戦力
先の例では次のようになります。
(10 - x) = (8 - y) Y軍が全滅すると (10 - x) = (8 - 0) x = 10 - 8 = 2
このように第1法則では、大きなほうから少ないほうを引いた差分が最終結果となります。
ランチェスターの第2法則では、第1法則と同様に、戦力の大きなほうが勝ちます。 しかし、第2法則では、勝利したほうの残存戦力が大きく異なります。
第2法則では、戦力の2乗の差の平方根で残存戦力を予測することが出来るモデルです。
例えば、X軍の10000人とY軍の8000人で戦うとします。 この結果は、集団戦となり戦力の2乗の差の平方根で残存戦力が規定され、√(10000^2 - 8000^2) = 6000ということで、多勢のX軍の兵が6000人も残るということです。これが第1法則ならば10000-8000 = 20000 となりX軍には2000人しか残りません。 第1法則の場合よりも大戦力側の優位が大きくなります。
式で表すと以下のようになります。
(x0^2 - x^2) = (y0^2 - y^2) x0: X軍の初期戦力 x : X軍の残存戦力 y0: Y軍の初期戦力 y : Y軍の残存戦力
先の例では次のようになります。
(10000^2 - x^2) = (8000^2 - y^2) Y軍が全滅すると (10000^2 - x^2) = (8000^2 - 0) x = √(10000^2 - 8000^2) = 6000
このように第2法則では、大きなほうの2乗から少ないほうの2乗を引いた差分の平方根が最終結果となります。
ランチェスターの第1法則と第2法則に則って作戦を考えると、戦力の多い状況でも少ない状況でも戦い方を有利にすることができるかもしれません。
自分の戦力が少ない場合には、ランチェスターの第1法則に該当するような一騎打ちのような状況になんとか持ち込みます。 しかし、所詮は寡兵ですから最初に戦力が減り決着が付く前になんとか撤退しなければなりません。 戦力の減り方は第2法則で戦うよりは遥かにすくないので、なんとかボカンと全力で一撃を食らわせたところで撤退するのがよい作戦でしょう。 最後の一撃に相手は用心して、追撃の手が緩むかもしれません。うまくいけば組し難い相手と思わせて今後の戦いの状況にもよい影響があるかもしれません。
次に、自分の戦力が多い場合には、ランチェスターの第2法則に該当するような集団戦法でターゲットを絞った攻撃に徹しましょう。 こちらが多数ならば力押しで戦っても相手を圧倒できます。 最初はなかなか相手も強気でしょうが、そこで弱気にならずに攻め続ければ、目に見えて敵の戦力が減り始めます。 その状況で相手を逃がさず追い詰めれば決定的な損失を与えて勝利することができます。
また、自分の戦力の多少に関わらず、相手の戦力をうまく分断して細かく分けることができれば、自分優位の第2法則の状況に持ち込むことができます。この状況に従って相手を各個撃破すれば確実な勝利を掴むことができるでしょう。
ランチェスターの第1法則の微分方程式を以下に示します。
dx -- = P - a * n - b * x dt dy -- = Q - c * n - d * y dt
Pはx軍のQはy軍の戦力増加率です。
a はy軍のc はx軍の武器性能です。
nは、一定時間内にどれだけの損害が出るかを示す定数です。
b はx軍のd はy軍の戦闘以外での戦力減少率です。
これらのパラメターを変更して、途中で援軍が増える前提でPやQを1.1などの1以上の値にするとか、 a やc を1以外にして、武器性能に差をつけるとか b やd を0以外にして、士気の低い軍からの脱走等をシミュレートすると面白いでしょう。
戦力10000対8000のランチェスター第1法則に従った戦いのシミュレートを以下のソースで行います。
/*
* ランチェスターの第一法則
* 10000 vs. 8000
*/
? ::sys <PrintResultOff>
<letf #P = 1>
<letf #Q = 1>
<letf #a = 1>
<letf #b = 0>
<letf #c = 1>
<letf #d = 0>
<letf #ni = 4000>
<setVar var_n #ni>
<letf #xi = 10000>
<setVar var_x #xi>
<letf #yi = 8000>
<setVar var_y #yi>
<print "t,x,y">
::sys <ODE (#t 0 3 0.01)
<var_x #x>
<var_y #y>
<var_n #n>
<letf #'dx/dt' = #P - #a * #n - #b * #x>
::sys <integral #x2 #'dx/dt' #xi>
<letf #'dy/dt' = #Q - #c * #n - #d * #y>
::sys <integral #y2 #'dy/dt' #yi>
(<comparef #x2 <= 0> <setVar var_x 0> <setVar var_n 0>
| <setVar var_x #x2> )
(<comparef #y2 <= 0> <setVar var_y 0> <setVar var_n 0>
| <setVar var_y #y2>)
<var_x #x3> <var_y #y3>
<print #t "," #x3 "," #y3>
>
;
最初に定数P, Q, a, b, c, dを設定しています。
Pはx軍のQはy軍の戦力増加率です。ここではどちらも途中では増加しないとして1にします。
aはy軍のcはx軍の武器性能です。ここではどちらも同等として1にします。
nは、一定時間内にどれだけの損害が出るかを示す定数です。ここではグローバル変数var_nに4000で設定します。
bはx軍のdはy軍の戦闘以外での戦力減少率です。ここではそれはないと仮定して0にします。
var_xにはx軍の初期値10000, var_yにはy軍の初期値8000を設定しています。
<print "t,x,y">では、CSV形式(カンマで区切られた形式)で、最初の行であるt,x,yを表示します。
ODE述語の中では、対象の微分方程式を数値解析的に計算していきます。 この引数を見ると、0 から 3 まで 0.01 刻みで微分方程式を計算するように設定されています。
ODE述語の中の処理では、まずvar_x, var_y, var_nから、x軍の現在の数#x, y軍の現在の数#y, 定数#nを取り出します。
#'dx/dt'は変数であり、微分方程式の値を計算して、次のintegral述語で積分して結果を#x2変数に設定します。
#'dy/dt'も同様であり、微分方程式の値を計算して、次のintegral述語で積分して結果を#y2変数に設定します。
次の構文は、x2が0より小さくなった場合、つまり0になって絶滅した場合には負の数にならないようにしています。
(<comparef #x2 <= 0> <setVar var_x 0> <setVar var_n 0>
| <setVar var_x #x2> )
comparefで0と比較し0以下ならばvar_xとvar_nを0に設定しています。それ以外の場合である正の数ならば#x2の値をグローバル変数var_xに書き戻します。
#y2も同様に負の数の場合は0に設定し、正の数ならば#y2の値をグローバル変数var_yに書き戻します。
最後にグローバル変数var_x, var_yの値をprint述語で表示して、CSV形式で出力します。
ソースをlanchester1.decという名前で保存して実行します。
$ descartes lanchester1.dec t,x,y 0 , 10000 , 8000 0.01 , 9960.01 , 7960.01 0.02 , 9920.02 , 7920.02 0.03 , 9880.03 , 7880.03 0.04 , 9840.04 , 7840.04 0.05 , 9800.05 , 7800.05 0.06 , 9760.06 , 7760.06 0.07 , 9720.07 , 7720.07 0.08 , 9680.08 , 7680.08 0.09 , 9640.09 , 7640.09 0.1 , 9600.1 , 7600.1 0.11 , 9560.11 , 7560.11 0.12 , 9520.12 , 7520.12 0.13 , 9480.13 , 7480.13 0.14 , 9440.14 , 7440.14 0.15 , 9400.15 , 7400.15 ... 途中略 ... 2.87 , 1936.2 , 0 2.88 , 1936.21 , 0 2.89 , 1936.22 , 0 2.9 , 1936.23 , 0 2.91 , 1936.24 , 0 2.92 , 1936.25 , 0 2.93 , 1936.26 , 0 2.94 , 1936.27 , 0 2.95 , 1936.28 , 0 2.96 , 1936.29 , 0 2.97 , 1936.3 , 0 2.98 , 1936.31 , 0 2.99 , 1936.32 , 0 3 , 1936.33 , 0
カンマで区切られた、時間, x軍の数, y軍の数がCSV形式で順に出力されます。
以下のように、lanchester1.csvという名前で結果を保存してみましょう。
$ descartes lanchester1.dec > lanchester1.csv
このように保存されたファイルは表計算ソフトで使えます。 Windowsならばlanchester1.csvをダブルクリックしただけでEXCELで開くことができます。
EXCELで読み込んでから、グラフ化したものを次に示しましょう。
(グラフ化する方法は、お持ちの表計算プログラムの方法に従ってください。)
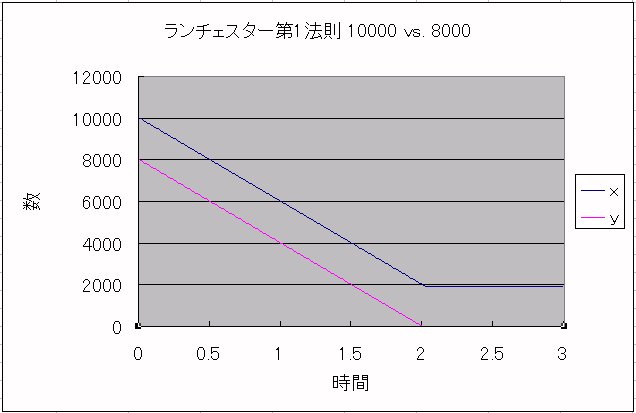
第1法則では、両軍の減少は直線で減っていきます。
そして最終的には両軍の差分である10000-8000の2000のx軍が残っています。
ランチェスターの第2法則の微分方程式を以下に示します。
dx -- = P - a * y - b * x dt dy -- = Q - c * x - d * y dt
Pはx軍のQはy軍の戦力増加率です。
a はy軍のc はx軍の武器性能です。
b はx軍のd はy軍の戦闘以外での戦力減少率です。
第1法則との違いは定数nが無くなって変わりに a * n の項が a * y に、c * n の項が c * x に変わっています。
その他の定数は、第1法則と同じなので対比してみてください。
戦力10000対8000のランチェスター第2法則に従った戦いのシミュレートを以下のソースで行います。
/*
* ランチェスターの第二法則
* 10000 vs. 8000
*/
? ::sys <PrintResultOff>
<letf #P = 0>
<letf #Q = 0>
<letf #a = 1>
<letf #b = 0>
<letf #c = 1>
<letf #d = 0>
<letf #xi = 10000>
<setVar var_x #xi>
<letf #yi = 8000>
<setVar var_y #yi>
<print "t,x,y">
::sys <ODE (#t 0 3 0.01)
<var_x #x>
<var_y #y>
<letf #'dx/dt' = #P - #a * #y - #b * #x>
::sys <integral #x2 #'dx/dt' #xi>
<letf #'dy/dt' = #Q - #c * #x - #d * #y>
::sys <integral #y2 #'dy/dt' #yi>
(<comparef #x2 <= 0> <setVar var_x 0> | <setVar var_x #x2>)
(<comparef #y2 <= 0> <setVar var_y 0> | <setVar var_y #y2>)
<var_x #x3> <var_y #y3>
<print #t "," #x3 "," #y3>
>
;
第1法則のソースと比べて違いは定数nが無くなっただけです。 「2.3.2.1.2 ランチェスター第1法則 ソース解説」と比較して見てください。
ソースをlanchester2.decという名前で保存して実行します。
$ descartes lanchester2.dec t,x,y 0 , 10000 , 8000 0.01 , 9920 , 7900 0.02 , 9840.33 , 7800.27 0.03 , 9762 , 7701.6 0.04 , 9684.32 , 7603.46 0.05 , 9607.96 , 7506.35 0.06 , 9532.25 , 7409.76 0.07 , 9457.83 , 7314.19 0.08 , 9384.05 , 7219.12 0.09 , 9311.55 , 7125.03 0.1 , 9239.67 , 7031.43 0.11 , 9169.04 , 6938.79 0.12 , 9099.04 , 6846.63 0.13 , 9030.26 , 6755.41 0.14 , 8962.1 , 6664.65 ... 途中略 ... 2.87 , 5934.38 , 0 2.88 , 5934.38 , 0 2.89 , 5934.38 , 0 2.9 , 5934.38 , 0 2.91 , 5934.38 , 0 2.92 , 5934.38 , 0 2.93 , 5934.38 , 0 2.94 , 5934.38 , 0 2.95 , 5934.38 , 0 2.96 , 5934.38 , 0 2.97 , 5934.38 , 0 2.98 , 5934.38 , 0 2.99 , 5934.38 , 0 3 , 5934.38 , 0
カンマで区切られた、時間, x軍の数, y軍の数がCSV形式で順に出力されます。
以下のように、lanchester2.csvという名前で結果を保存してみましょう。
$ descartes lanchester2.dec > lanchester2.csv
このように保存されたファイルは表計算ソフトで使えます。
EXCELで読み込んでから、グラフ化したものを次に示しましょう。

第2法則では、y軍が大幅に減少していくのに対して、x軍の減少の仕方が途中から緩やかになります。
そして最終的には両軍の2乗の差分である 10000^2 - 8000^2 の平方根である 6000 の x 軍が残っています。
同じ条件でx軍の残存戦力が2000まで減ってしまった第1法則の場合と比べて、優勢であるx軍が圧倒的に有利であることがわかります。
[PageInfo]
LastUpdate: 2012-08-30 22:19:39, ModifiedBy: hniwa
[License]
![]() Creative Commons 2.1 Attribution
Creative Commons 2.1 Attribution
[Permissions]
view:all, edit:login users, delete/config:login users